Tag: deep-learning

What Curve Am I Riding?

Me teaching the youth how to wire up lasers in 2014

If you think programming is hard now. You are listening to the wrong gurus. Programming computers has never been easier. I will not justify that statement in a single breathe, and this is kind of a venting post, so please take with a grain of salt.

Exponential Complexity

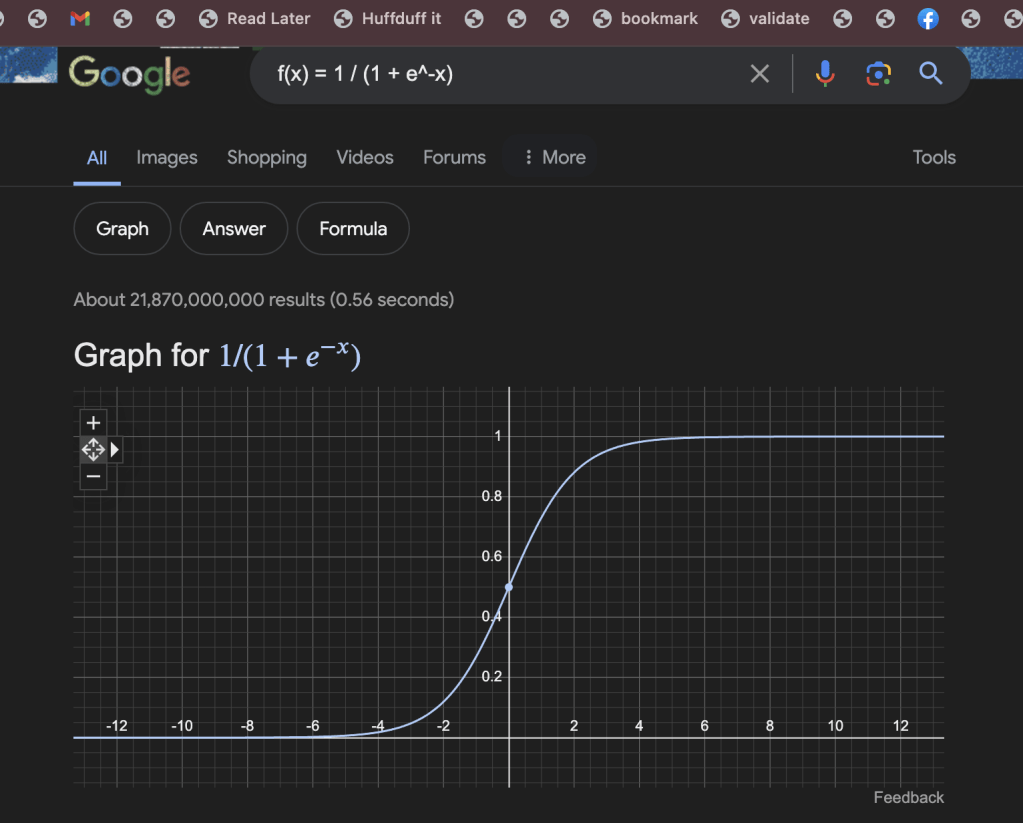
Where are we in this sigmoid? What is a sigmoid? Lets ask our AI brethren.

A sigmoid is a special type of mathematical function that is often used in machine learning and data analysis. It looks like an “S” shape, with the middle part being steep and the two ends being flat. Sigmoids have a really useful property: they can take any number as input, but they always output a value between 0 and 1.

Here’s an example of a sigmoid function:

f(x) = 1 / (1 + e^-x)

This formula might look scary, but it’s actually pretty simple. The “e” in the formula is just a special number called Euler’s number (it’s about 2.71828). The “-x” inside the parentheses means that we take the opposite of whatever number we plug in for x. So if x is 5, then -x would be -5.

e^-x == 1/e^x

-rob

When we plug a negative number into this formula, we get a number very close to 0. When we plug in a positive number, we get a number very close to 1. And when we plug in zero, we get 0.5. So you can see how the sigmoid function maps any input number to a value between 0 and 1.

-Mixtral22b

sigmoidDownload

Sigmoids & Friends

I ❤ functions. Sigmoids are very cool. I actually used a sigmoid back when I did my Genetic Algorithm Caterpillar thing for undergrad a decade ago. I used a slightly different but same effect.

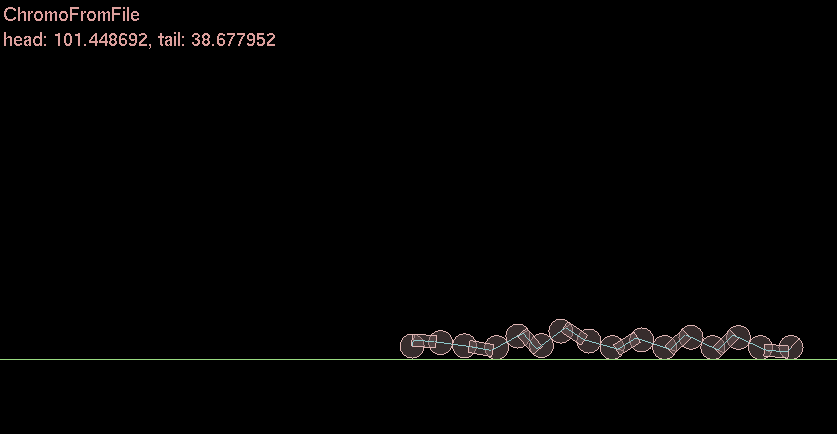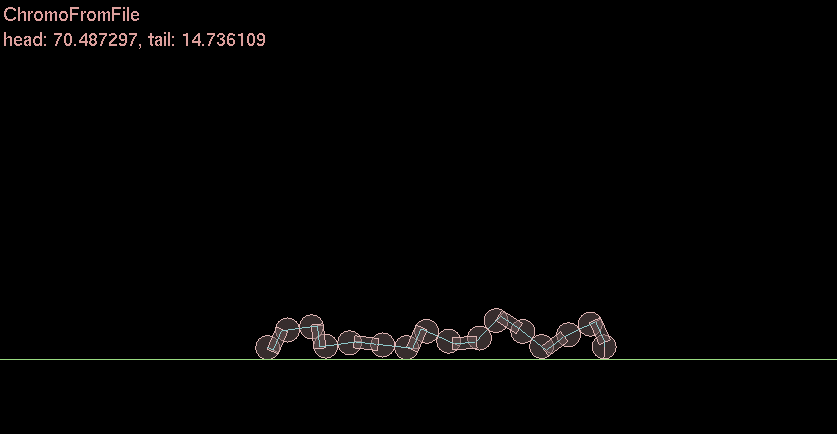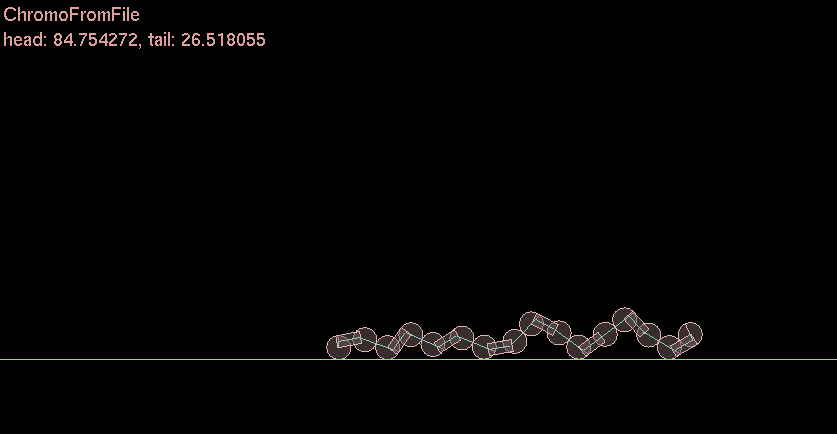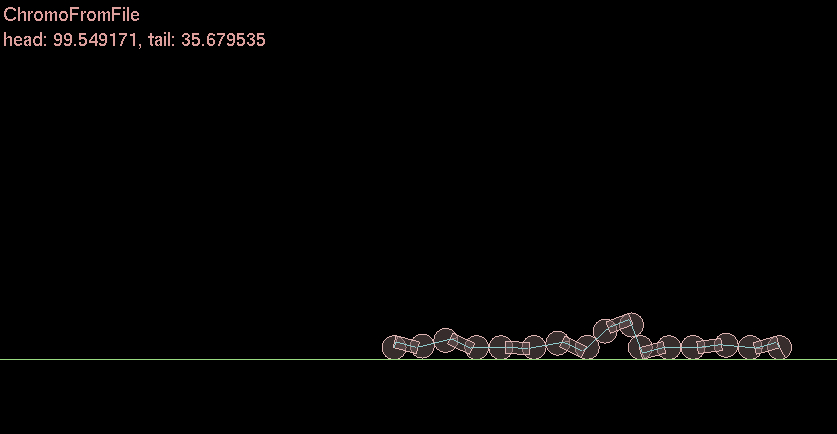
Creepture circa 2013 – sigmoid activation for network between “muscles”
Excerpt from Creepture paper (appendix)

Ok so why is this useful [late update]

In neural networks in order for a neuron to become excited and “fire” the signals into the neuron through a “synapse” must be added and the fed to a sigmoid function. This will fire a zero or one to the other connected neurons. And then each layer this happens and is forward or backward propagated through the network to the output/input.

In this simple caterpillar example each joint represents a “motor” or “muscle” that is activated by the sigmoid. Zero or One. Move + Stay

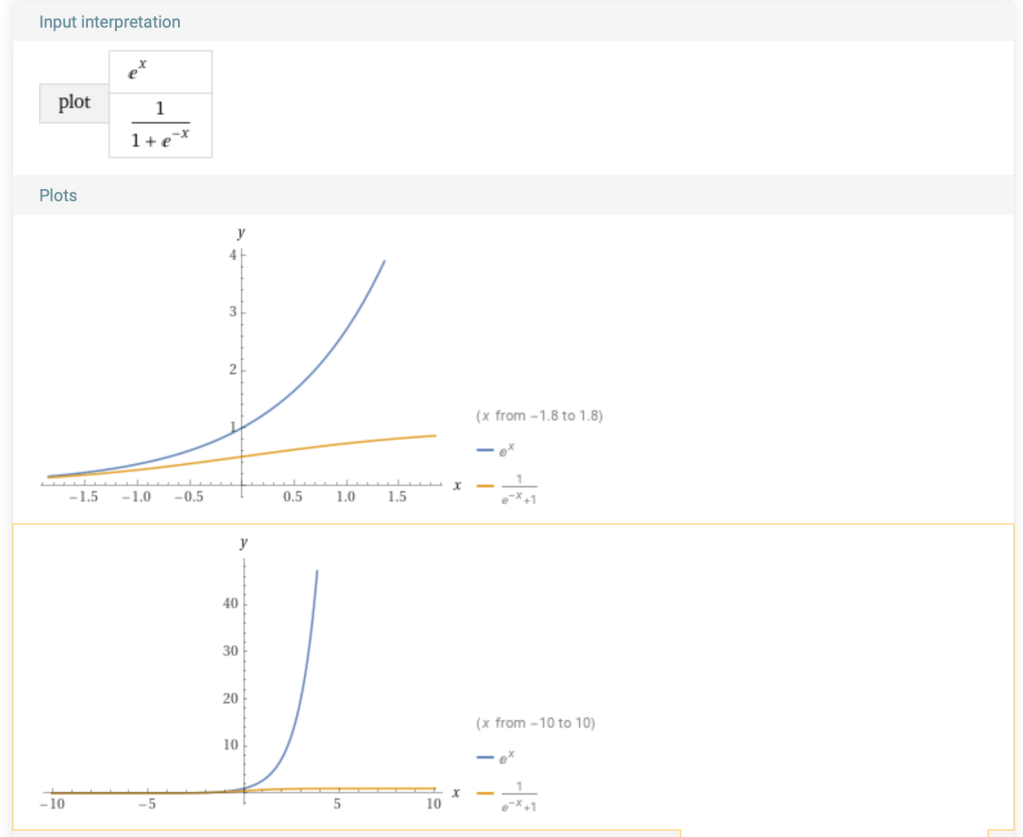
So what does this have to do with the exponential complexity topic. Lets talk e^x

Put them into your graphing calculators. play around with sweep.

The Natural Number

e has this special feature. It is often called “Euler’s Number” approximately 2.718…

Deriving it links to compound interest. So you know it’s good. It is irrational meaning you cannot represent it fully with a decimal or fraction. Go take a look at your precalculus books 🙂

(e^x) != (1 / (1 + e^-x))

You can be tricked you are in an exponential function. You might be in a sigmoid 😦

Wolframe output: https://www.wolframalpha.com/input?i=plot+e%5Ex+vs+%281%2F%281%2Be%5E-x%29%29

Developing Now Has Never Been Easier

With the amount of documentation, tutorials, influencers, companies shilling products…. I get it. Your signal to noise ratio is approaching zero. But let me give you some signal in that numerator.

  • Go back to first principles when possible (the math!!!)
  • Avoid new language (versions), frameworks, fads/trends
    • Unless you understand this could be completely a waste of time and you are ok with it. schedule your treks.
  • Remember programming has a fashion sine curve. If you stick around long enough it will become advant-garde again 🙂

Focus on product, use your product, programmers that are NOT project/product driven are doomed to make buttons that nobody clicks. Make something so valuable and ship it that so that if it goes down, PEOPLE CARE.

Appendix

report-1Download

Sea Change

I’ve been promised Virtual Reality and Artificial Intelligence (AI) all my life. I bought the Power Glove. It was all mostly just hype and small toys that never stuck. But current iterations?

What we are seeing now with AI with regards to Large Language Models (LLMs such as GPT) and Stable Diffusion (Image Generation) is nothing short of a change in how we use computers. Models, weights, and LoRas? are now the “Programs” we run.

I’ve spent last month with these products like InvokeAI and Ollama, they are wonderful, but they aren’t even close to where we will be in 2 years for a consumer. But I can’t help but think of the giant foundational models trained on the entire human corpus being compressed into little tiny chips that can be queried anywhere as some type of “Holographic” computing.

I can understand why that one google engineer freaked out talking to internal chatbot.

“I think, therefore I am” is a famous philosophical statement made by René Descartes in his Meditations on First Philosophy. The statement is often translated from the original French as “Cogito, ergo sum,” and it is meant to express the idea that the very act of doubting one’s existence serves as proof of one’s own consciousness.

In other words, if you are able to think about whether or not you exist, then you must exist in some form in order to have that thought. This statement has been interpreted and debated by philosophers for centuries, but at its core, it is a powerful reminder of the connection between thinking and being.

Mistral24b

Philosophy aside and lets talk Hardware

We are in the “Mainframe” era of AI. These models literally take up rooms (rows of racks in a datacenter) and it seems its One Big GPU per User at a time. I’m trying to fathom what it takes to support a Copilot or ChatGPT at Microsoft and oAI’s scale.

As you see now the problem with size is combination of power and memory bandwidth, but these will be solved with tricks like they always are. INT8 quantization is so hilariously simple optimization that I’m quite shocked it works so well.

Overview of quantization that I will spend the rest of the month fact checking…

Compressing the weights of neural networks from floating-point to int8 (also known as quantization) can significantly reduce the computational requirements and memory footprint of deep learning models, making them more suitable for deployment on low-power hardware such as mobile devices or embedded systems.

The general idea behind weight compression is to represent the weights of a neural network using fewer bits than their original floating-point representation. By reducing the precision of the weights, it is possible to significantly reduce the storage requirements and computational complexity of the model. In particular, int8 quantization involves representing the weights as 8-bit integers rather than 32-bit or 64-bit floating-point numbers.

There are several steps involved in compressing neural network weights from floating-point to int8:

  1. Weight normalization: This step involves scaling the weights of the neural network so that they fit within the range of an 8-bit integer. This is typically done by computing the maximum absolute value of the weights and then scaling them accordingly.
  2. Quantization: This step involves converting the normalized weights from floating-point to int8 format. There are several methods for doing this, including linear quantization and logarithmic quantization.
  3. Decomposition: In some cases, it may be possible to decompose the weight matrix of a neural network into smaller matrices that can be more easily compressed. This is known as low-rank decomposition or tensor decomposition.
  4. Pruning: This step involves removing unnecessary connections between neurons in the neural network, further reducing the computational requirements and memory footprint of the model.
  5. Codebook generation: In some cases, it may be possible to generate a codebook that maps int8 values back to their original floating-point values. This can help improve the accuracy of the compressed model.
  6. Model fine-tuning: After compressing the weights of a neural network, it is typically necessary to fine-tune the model to ensure that its performance is not significantly degraded. This can be done using techniques such as knowledge distillation or iterative quantization.

Overall, compressing neural network weights from floating-point to int8 format can greatly improve the performance and energy efficiency of deep learning models on low-power hardware. However, it requires careful consideration of factors such as weight normalization, quantization, decomposition, pruning, codebook generation, and model fine-tuning in order to ensure that the compressed model retains its accuracy and performance.

Mistral24b

Google sells the Coral TPU system that is a usb accelerator that is capable of few TeraFlops (TOPS – Trillion Operations per Second). Great for old school CNN style networks but pretty much useless for the current generation of AI models of Transformers and giant Video RAM (VRAM 24GB+)

I’m awaiting the LLM/StableDiffusion version of the Coral TPU or Jetson Nano (NVIDIA)

Make sure you board is waxed, this is going to be a giant wave of VR and AI coming in this next 3 years.